Introduction
단절점이란 제거했을때 연결되어있던 그래프가 둘 이상으로 나눠지는 그래프를 말한다.
단절점을 가장 naive 하게 구하는 방법은 모든 정점에 대해 그 정점을 제거할 경우 connected component가 증가하는지를 탐색을 통해 확인하면 된다. 이 경우 시간복잡도는 $O(V^2)$ 가 된다.
하지만 단절점의 특징을 사용해서 탐색 한번으로 $O(V)$ 단절점을 구할 수 있다.
단절점 구하기
아래 그림을 보자.
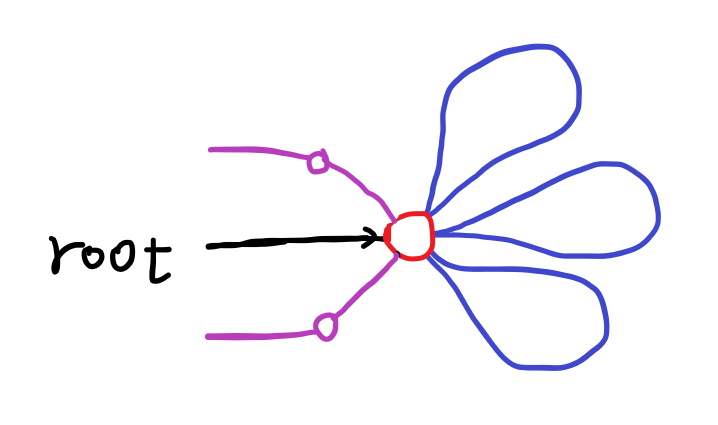
위 그림은 root를 시작점으로 dfs를 도는 중간 과정을 나타낸다.
빨간색 정점 : 현재 보고있는 정점이다.
검은색 간선 : 바로 직전에 타고(?) 온 간선으로 root 쪽에서 왔다는것을 나타낸다.
보라색 정점 : root 쪽에서 이미 탐색을 완료한 정점이다.
파란색 덩어리(?) : 아직 방문하지 않은 connected component로, 빨간색의 dfs number보다 더 작은 dfs number을 가진 정점과는 절대! 연결되어 있지 않아야 된다. (빨간색 정점을 제거해도 파란색 덩어리 내에서 서로 연결되어 있다.)
여기서 dfs number들을 비교해 보면 (root 정점, 보라색 정점) < (빨간색 정점) < (파란색 덩어리들) 인 것을 알 수 있다.
그럼 빨간색 정점이 단절점이 될 조건을 살펴보면, 파란색 덩어리가 한개 이상 있으면 단절점 이라는 것을 알 수 있다.
특정 점에서 dfs를 돌고 난 후 리턴 값을 '그 정점에서 탐색을 돌았을때 만나는 가장 작은 dfs number' 로 정의하자.
그러면 파란색 덩어리를 구별하는 방법은, 탐색의 리턴값이 현재 자신의 dfs number보다 같거나 클 경우 이다.
다만, 이러한 방법으로는 root의 단절점 여부는 판단할 수 없다.
root 정점의 단절점 여부는, root 정점에서 탐색을 돈 횟수가 2 이상이면 단절점으로 판단한다.
이는 조금만 생각해보면 당연함을 알 수 있다.
코드
코드는 이 문제를 기준으로 작성되었다.
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int v, e, num[10001];
bool cutable[10001] = { false };
vector<int> adj[10001];
int dfsNum;
int dfs(int idx, int pre) {
num[idx] = dfsNum++;
int minTime = num[idx], maxTime = -1, cnt = 0;
for (int i = 0; i < adj[idx].size(); i++) {
int nex = adj[idx][i];
if (nex == pre) continue;
int dfsTime;
if (num[nex] == 0) {
dfsTime = dfs(nex, idx);
maxTime = max(maxTime, dfsTime);
cnt++;
}
else
dfsTime = num[nex];
minTime = min(minTime, dfsTime);
}
if (pre != -1)
cutable[idx] = maxTime >= num[idx];
else
cutable[idx] = cnt >= 2;
return minTime;
}
int main(void) {
scanf("%d %d", &v, &e);
for (int i = 0; i < e; i++) {
int a, b;
scanf("%d %d", &a, &b);
adj[a].push_back(b);
adj[b].push_back(a);
}
for (int i = 1; i <= v; i++) {
if (num[i] == 0) {
dfsNum = 1;
dfs(i, -1);
}
}
int pointCnt = 0;
for (int i = 1; i <= v; i++)
pointCnt += (int)cutable[i];
printf("%d\n", pointCnt);
for (int i = 1; i <= v; i++) {
if (cutable[i])
printf("%d ", i);
}
printf("\n");
return 0;
}'PS' 카테고리의 다른 글
| Mo's Algorithm (0) | 2023.08.14 |
|---|---|
| Sqrt Decomposition (0) | 2023.08.13 |
| Master Theore (0) | 2023.08.11 |
| Euler tour technique (0) | 2023.08.08 |
| monotone queue (0) | 2023.08.05 |
