문제
무한한 격자판이 있다고 하자.
각 셀은 0 또는 1의 상태를 가질 수 있다.
각 셀은 단위 시간 마다 다음 규칙에 따라서 상태가 바뀐다.
- $t$ 시간에 어떤 셀의 위치를 $(r,c)$ 라고 할 때 $(r+1,c)$와 $(r,c+1)$ 위치의 셀이 모두 $1$ 이면 $t+1$시간에 $(r,c)$ 셀의 상태는 1이다.
- $t$ 시간에 어떤 셀의 위치를 $(r,c)$ 라고 할 때 $(r+1,c)$ 또는 $(r,c+1)$ 위치의 셀이 $0$ 이면 $t+1$시간에 $(r,c)$ 셀의 상태는 0이다.
초기에 상태가 1인 셀들이 유한하다고 할 때, 시간이 충분히 흐른다면 모든 셀들의 상태가 0이 됨을 보이시오.
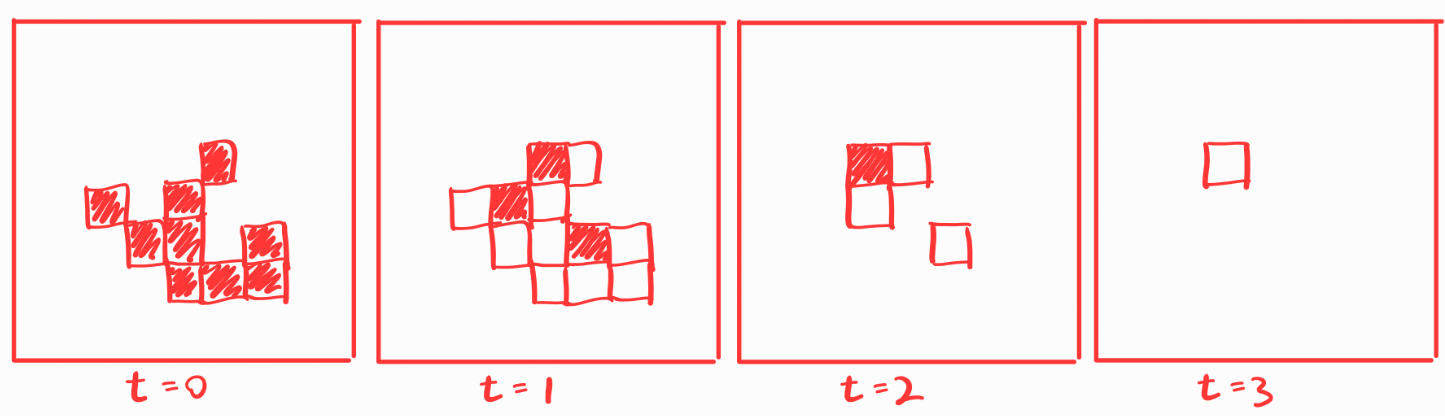
증명
$t$ 시간에 1인 셀의 개수를 $n_t$, 초기에 1인 셀의 개수를 $m=n_0$, 각 셀의 상태를 $s(r,c)$ 라고 하자.
그리고 다음과 같은 3가지 타입의 셀들을 생각해보자.
$$\begin{align}
s_a(r,c) &= s(r+1,c) \cdot s(r,c+1) \\
s_b(r,c) &= s(r+1,c) \cdot (1- s(r,c+1)) \\
s_c(r,c) &= (1- s(r+1,c) ) \cdot s(r,c+1)
\end{align}$$
- $s_a(r,c)$ : 오른쪽, 아래 셀 모두가 1인 셀들을 나타낸다.
- $s_b(r,c)$ : 아래 셀이 1이고 오른쪽 셀이 0인 셀들을 나타낸다.
- $s_c(r,c)$ : 아래 셀이 0이고 오른쪽 셀이 1인 셀들을 나타낸다.
그리고 시간 $t$에 $s_a(r,c)=1$인 셀의 개수를 $a_t$, $s_b(r,c)=1$인 셀의 개수를 $b_t$, $s_c(r,c)=1$인 셀의 개수를 $c_t$ 라고 하자.
이제 우리는 $a_t, b_t, c_t, n_t$ 간의 관계를 따질 것이다.
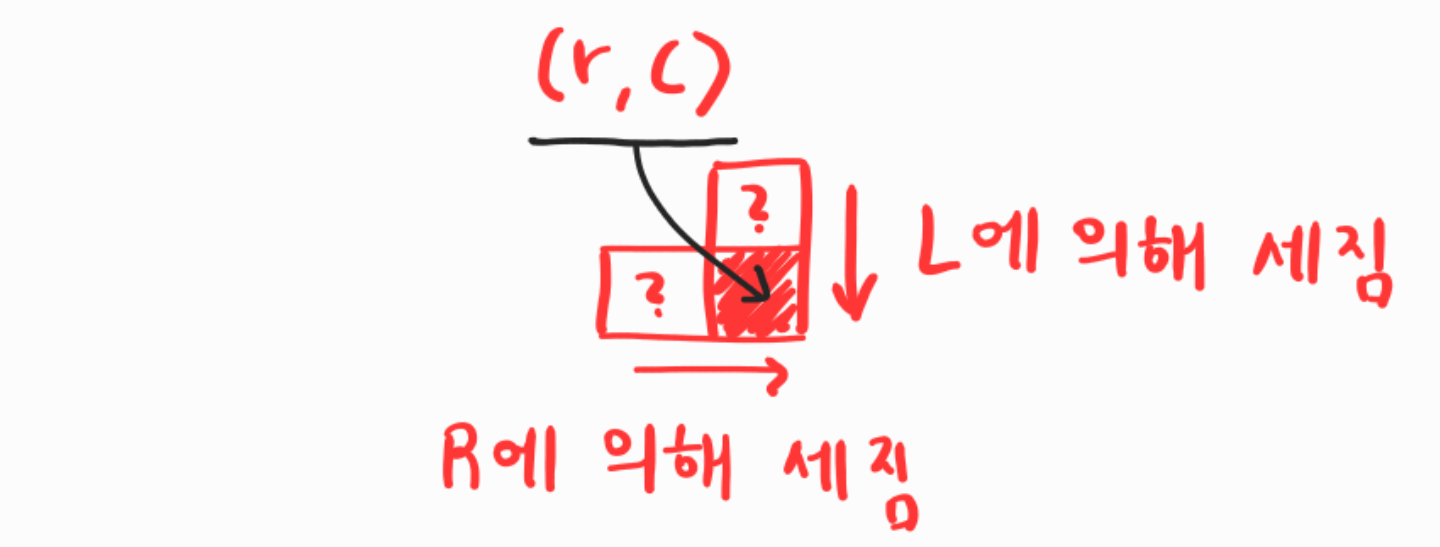
(아래가 1인 셀의 개수 + 오른쪽이 1인 셀의 개수)에 대해 생각해보자.
좀더 형식적으로는 $L= \{ (r,c) | s(r+1,c)=1 \; \forall \; r,c \}, \; R= \{ (r,c) | s(r,c+1)=1 \; \forall \; r,c \}$ 라고 할때 $|L|+|R|$을 나타낸다.
- 자명하게 $|L|+|R| = n_t+n_t = 2n_t$ 이 성립한다.
- 다음을 보자.
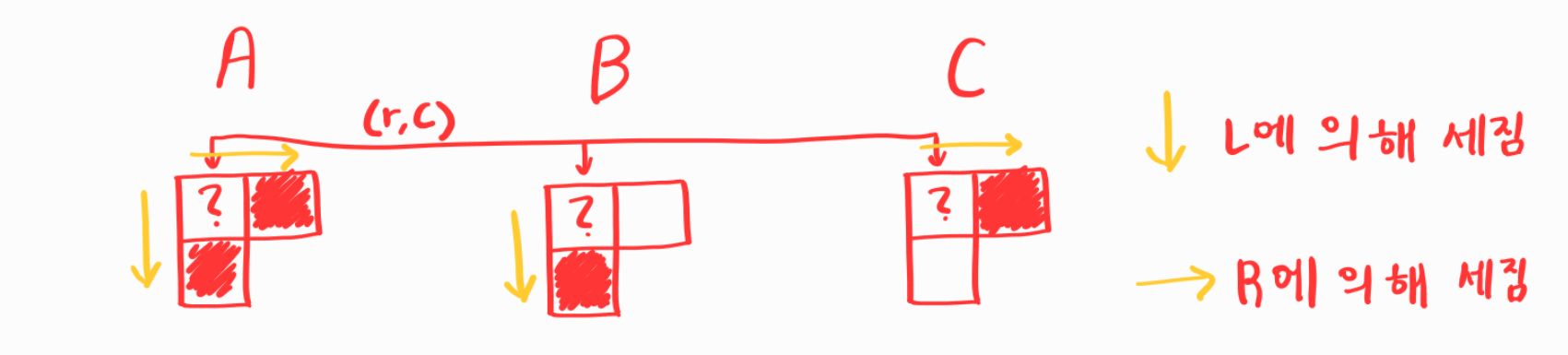
(1) $ s_a(r,c)=1 \lor s_b(r,c)=1 \lor s_c(r,c)=1 $ 가 거짓인 경우 : $(r,c) \notin L, (r,c) \notin R$ 이다.
(2) $ s_a(r,c)=1 \lor s_b(r,c)=1 \lor s_c(r,c)=1 $ 가 참인 경우 :
(a) $s_a(r,c)=1$가 참인 경우 $(r,c) \in L, (r,c) \in R$ 이다.
(b) $s_b(r,c)=1$ 가 참인 경우 $(r,c) \in L, (r,c) \notin R$ 이다.
(c) $s_c(r,c)=1$ 가 참인 경우 $(r,c) \notin L, (r,c) \in R$ 이다.
(참고) $s_a(r,c)=1, s_b(r,c)=1, s_c(r,c)=1 $ 중 어느 두개도 동시에 참일 수 없으므로 세 명제에 대해 진리집합들은
서로 독립집합이다.
(1)과 (2)의 (a), (b), (c) 에 의해 $|L|+|R| = 2a_t + b_t + c_t$ 이 성립한다.
1. 와 2. 에 의해 $a_t + \frac{b_t + c_t}{2} = n_t$ 이 성립한다.
그런데 문제의 규칙에 따라서 $a_t = n_{t+1}$ 도 성립한다.
그러므로 $n_t \geqslant n_{t+1} $ 가 성립하고, $n_t > 0$이면 $n_t>n_{t+1}$ 또한 성립한다.
($n_t > 0$ 인 경우 $ b_t + c_t > 0$인 것은 어렵지 않게 증명이 가능하다.)
$n_0=m$이고 $n_t > 0 \Rightarrow n_t>n_{t+1}$ 이므로 충분히 큰 $t$에 대해 $n_t=0$ 이라는 것은 수학적 귀납법으로 보일 수 있다.
'수학' 카테고리의 다른 글
| Quaternion 정리 (0) | 2023.11.29 |
|---|
문제
무한한 격자판이 있다고 하자.
각 셀은 0 또는 1의 상태를 가질 수 있다.
각 셀은 단위 시간 마다 다음 규칙에 따라서 상태가 바뀐다.
- $t$ 시간에 어떤 셀의 위치를 $(r,c)$ 라고 할 때 $(r+1,c)$와 $(r,c+1)$ 위치의 셀이 모두 $1$ 이면 $t+1$시간에 $(r,c)$ 셀의 상태는 1이다.
- $t$ 시간에 어떤 셀의 위치를 $(r,c)$ 라고 할 때 $(r+1,c)$ 또는 $(r,c+1)$ 위치의 셀이 $0$ 이면 $t+1$시간에 $(r,c)$ 셀의 상태는 0이다.
초기에 상태가 1인 셀들이 유한하다고 할 때, 시간이 충분히 흐른다면 모든 셀들의 상태가 0이 됨을 보이시오.

증명
$t$ 시간에 1인 셀의 개수를 $n_t$, 초기에 1인 셀의 개수를 $m=n_0$, 각 셀의 상태를 $s(r,c)$ 라고 하자.
그리고 다음과 같은 3가지 타입의 셀들을 생각해보자.
$$\begin{align}
s_a(r,c) &= s(r+1,c) \cdot s(r,c+1) \\
s_b(r,c) &= s(r+1,c) \cdot (1- s(r,c+1)) \\
s_c(r,c) &= (1- s(r+1,c) ) \cdot s(r,c+1)
\end{align}$$
- $s_a(r,c)$ : 오른쪽, 아래 셀 모두가 1인 셀들을 나타낸다.
- $s_b(r,c)$ : 아래 셀이 1이고 오른쪽 셀이 0인 셀들을 나타낸다.
- $s_c(r,c)$ : 아래 셀이 0이고 오른쪽 셀이 1인 셀들을 나타낸다.
그리고 시간 $t$에 $s_a(r,c)=1$인 셀의 개수를 $a_t$, $s_b(r,c)=1$인 셀의 개수를 $b_t$, $s_c(r,c)=1$인 셀의 개수를 $c_t$ 라고 하자.
이제 우리는 $a_t, b_t, c_t, n_t$ 간의 관계를 따질 것이다.
(아래가 1인 셀의 개수 + 오른쪽이 1인 셀의 개수)에 대해 생각해보자.
좀더 형식적으로는 $L= \{ (r,c) | s(r+1,c)=1 \; \forall \; r,c \}, \; R= \{ (r,c) | s(r,c+1)=1 \; \forall \; r,c \}$ 라고 할때 $|L|+|R|$을 나타낸다.
- 자명하게 $|L|+|R| = n_t+n_t = 2n_t$ 이 성립한다.
- 다음을 보자.
(1) $ s_a(r,c)=1 \lor s_b(r,c)=1 \lor s_c(r,c)=1 $ 가 거짓인 경우 : $(r,c) \notin L, (r,c) \notin R$ 이다.
(2) $ s_a(r,c)=1 \lor s_b(r,c)=1 \lor s_c(r,c)=1 $ 가 참인 경우 :
(a) $s_a(r,c)=1$가 참인 경우 $(r,c) \in L, (r,c) \in R$ 이다.
(b) $s_b(r,c)=1$ 가 참인 경우 $(r,c) \in L, (r,c) \notin R$ 이다.
(c) $s_c(r,c)=1$ 가 참인 경우 $(r,c) \notin L, (r,c) \in R$ 이다.
(참고) $s_a(r,c)=1, s_b(r,c)=1, s_c(r,c)=1 $ 중 어느 두개도 동시에 참일 수 없으므로 세 명제에 대해 진리집합들은
서로 독립집합이다.
(1)과 (2)의 (a), (b), (c) 에 의해 $|L|+|R| = 2a_t + b_t + c_t$ 이 성립한다.


1. 와 2. 에 의해 $a_t + \frac{b_t + c_t}{2} = n_t$ 이 성립한다.
그런데 문제의 규칙에 따라서 $a_t = n_{t+1}$ 도 성립한다.
그러므로 $n_t \geqslant n_{t+1} $ 가 성립하고, $n_t > 0$이면 $n_t>n_{t+1}$ 또한 성립한다.
($n_t > 0$ 인 경우 $ b_t + c_t > 0$인 것은 어렵지 않게 증명이 가능하다.)
$n_0=m$이고 $n_t > 0 \Rightarrow n_t>n_{t+1}$ 이므로 충분히 큰 $t$에 대해 $n_t=0$ 이라는 것은 수학적 귀납법으로 보일 수 있다.
'수학' 카테고리의 다른 글
| Quaternion 정리 (0) | 2023.11.29 |
|---|
